- 邮箱:
- 广东省广州市天河区88号
- 电话:
- /public/upload/system/2018/07/26/f743a52e720d8579f61650d7ca7a63a0.jpg
- 传真:
- /public/upload/system/2018/07/26/fe272790a21a4d3e1e670f37534a3a7d.png
- 手机:
- 13800000000
- 地址:
- 1234567890
本篇为课程CS229的补充材料Convex Optimization Overview[1]的笔记。许多机器学习方法如最小二乘法、logistic回归、支持向量机都可以归纳到凸优化问题的框架之下,并得到有效的解决。这篇文章主要对原凸优化讲义内容进行总结,并对部分定义证明进行适当的补充。下半部分为凸优化综述(下)
- 先验知识
- 凸集(Convex Sets)
- 凸函数
- 凸性的一阶条件(First Order Condition for Convexity)
- 凸性的二阶条件(Second Order Condition for Convexity)
- Sublevel Sets
- 凸函数的例子
- 凸优化问题中的全局最优值
范数
非正式地说,向量 的范数
是这个向量的长度的度量,以第二范数欧几里得范数为例,
,写成向量形式为
。更正式地说,范数是满足以下四个条件的任何函数
:
- 非负性:对于所有
,有
- 正定性:当且仅当
的时候
- 齐次性:对于所有
,
- 三角不等式:对于所有
,
仿射子空间、多面体、仿射变换以及仿射函数
定义表述如下:
- 仿射子空间(affine subspaces):给定矩阵
以及向量
,仿射子空间为集合
- 多面体(polyhedra):类似的,多面体为集合
;注意,此处的符号
表示逐元素不等,即
的结果所有位置上的值都小于向量
对应位置上的值
- 仿射变换(affine transformation):从
到
的变换
被称为仿射变换,其中
,
,
为常向量
- 仿射函数(affine function):仿射函数为仿射变换的一种特殊情况,当仿射变换中的
时,
,
都为常数;此外,如果将此处
中的截距
去掉,剩下的部分
被称为线性函数
二次函数的 矩阵
设二次函数 ,其中矩阵
为对称矩阵
。
可以进行如下展开:
先对
求导,以
项为例:
由此可以推出,对于整体而言
再求
的
矩阵:
由此可以推出,对于整体而言
为了方便记忆这些结论,可以将上述结论与单变量求导的情况进行类比,例如将
类比为
,将
类比为
矩阵求导总结:
定义:对于任何 ,
且
,若
成立,则称集合
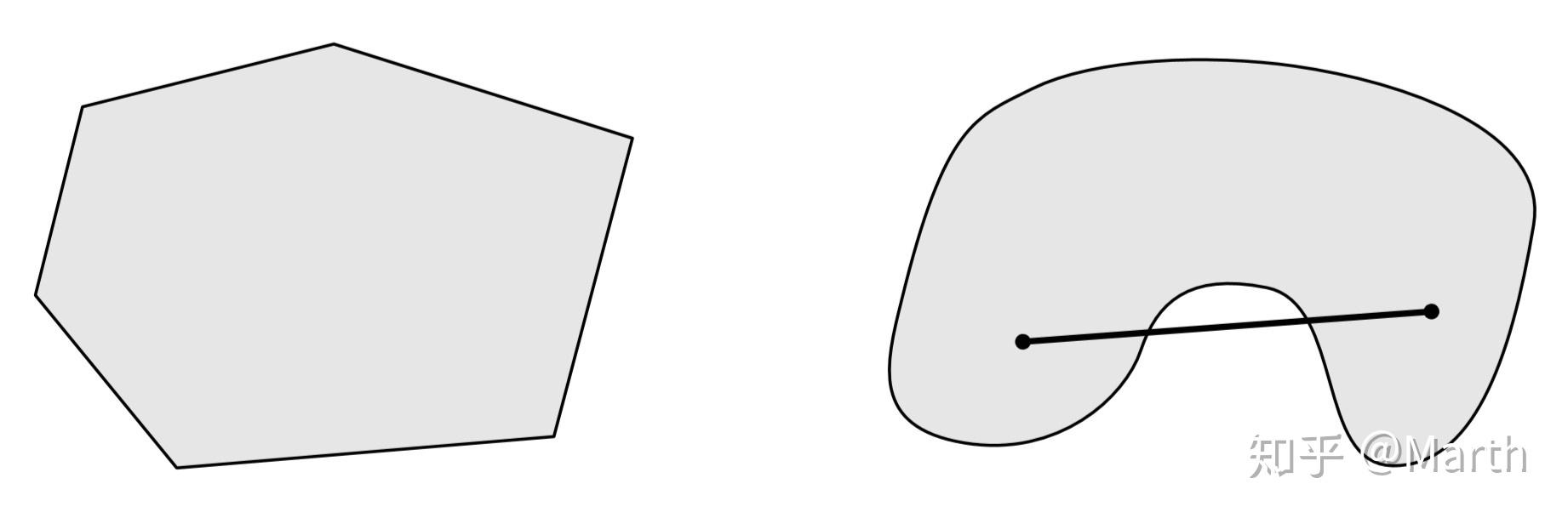
为凸的。
可以通过下面的图来直观地理解什么是凸集:对于凸集 中的任意两个元素
,用一条线段将这两个元素连起来,那么这条线段上的每个元素都属于
。
典型的凸集有:
- 实数向量
- 非负象限
- 范数球
:设存在
,
,
,且
,利用范数的齐次性以及三角不等式有
- 仿射子空间
- 多面体
- 凸集的交集:设集合
为凸集,那么它们的交集
也是凸集。需要注意,凸集的并集往往不是凸集
- 半正定矩阵:设存在两个半正定矩阵
,
,对于所有的
有
而其中
,
,所以
所以半正定矩阵也是凸集
证明集合属于凸集的关键在于明确原集合的定义,之后利用凸集的定义进行证明即可。
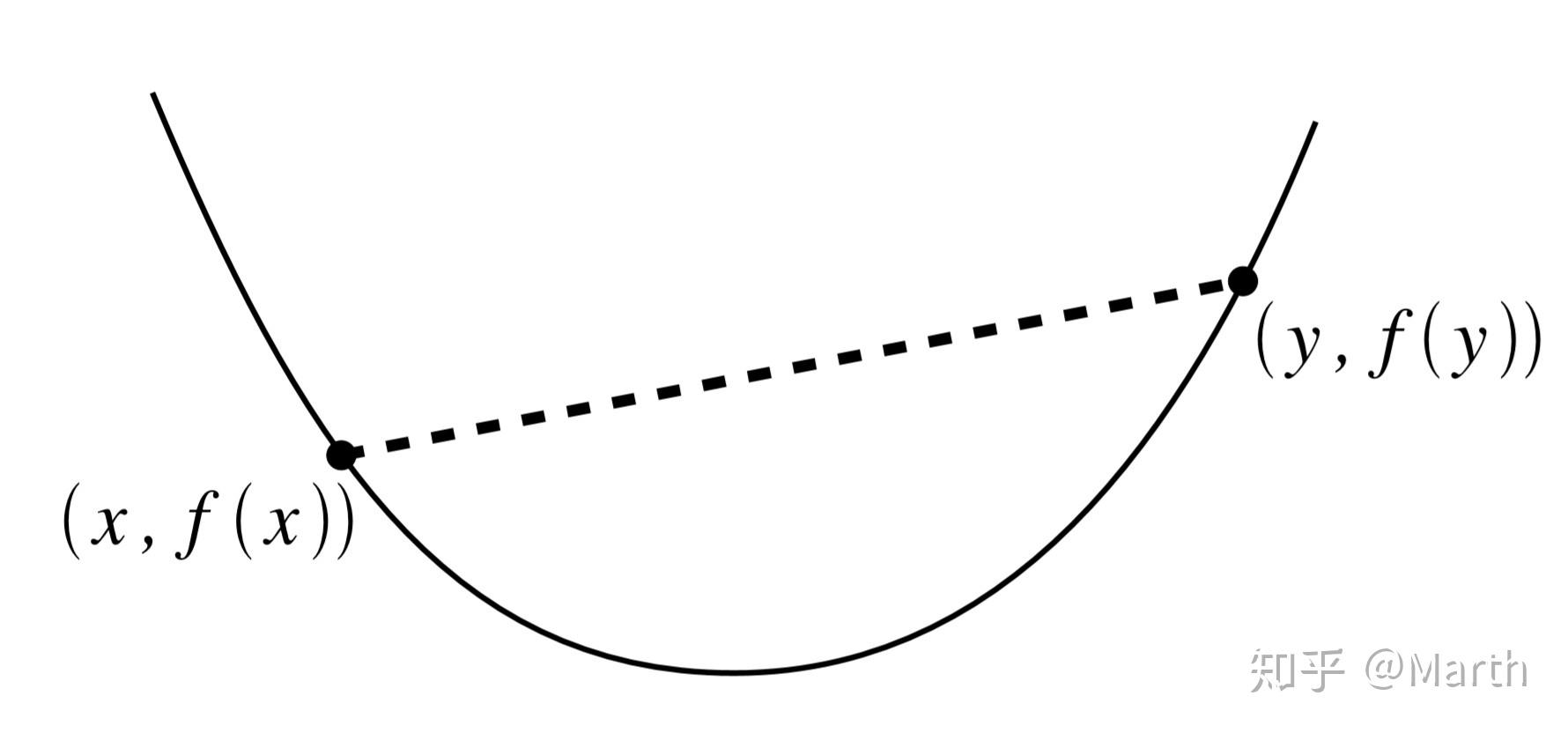
定义:对于函数 ,如果它的域
是一个凸集,并且对于所有
,
,有
那么函数
被称为凸函数。
可以通过下面的图来直观地理解什么是凸函数:如果取凸函数上的两点并在它们之间连一条线段,那么两点之间的函数部分都会在这条线段之下。
进一步定义,如果上述定义对 且
的条件成立,则称函数
为严格凸函数。如果函数
为凸的,则定义
为凹的,严格凹函数的定义以此类推。
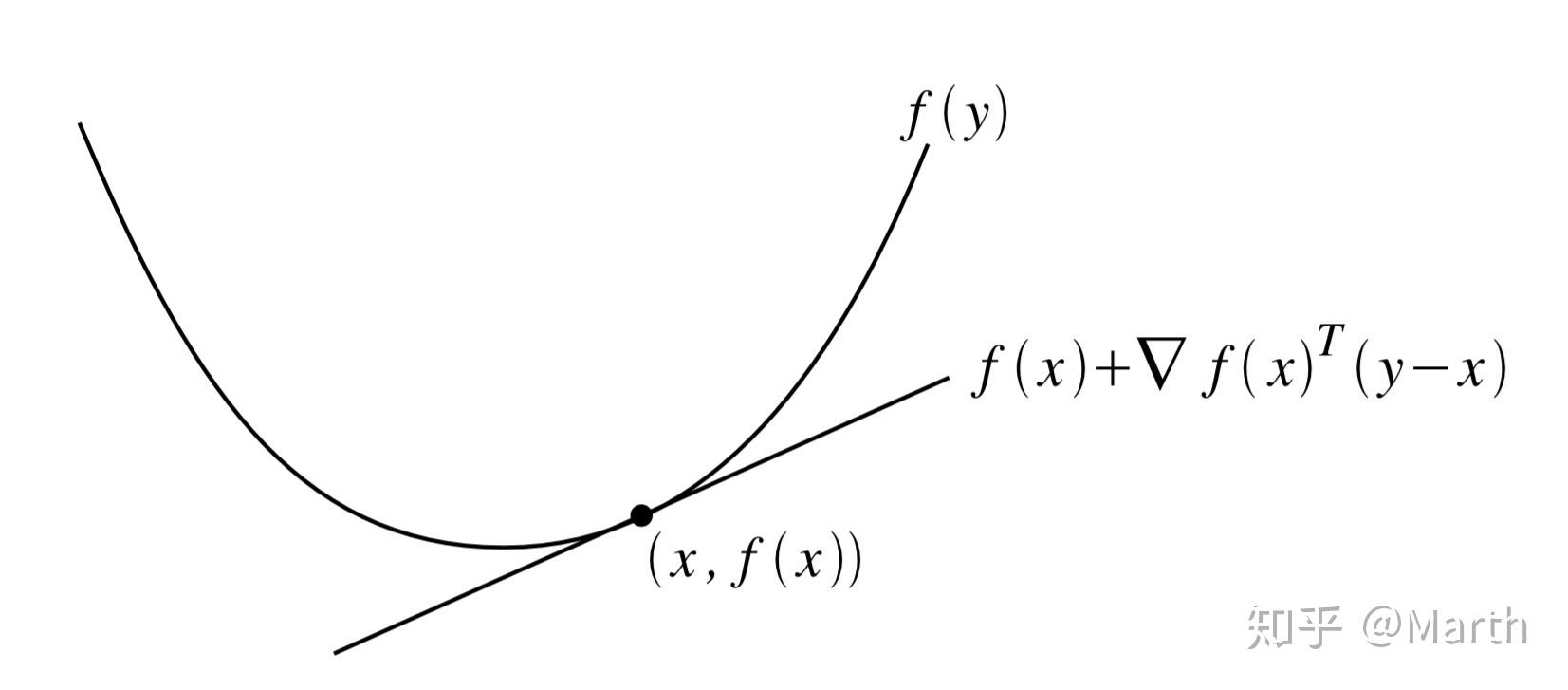
定义:假设函数 可微(即对于所有
,导数
恒存在),当且仅当
为凸集且对于所有
都成立的时候,可以称函数
是凸函数。
可以通过下面的图来直观地理解什么是凸性的一阶条件:对于凸函数上的任一点 ,它所在处的切平面永远在函数
下方。
凸性的一阶条件可以由凸函数的定义推导得到。凸函数的定义为(此处为了方便证明对变量 的顺序做了些许改动):
对这个式子的左边进行变换:
,再根据凸函数的定义有:
继续变换有:
令
,易知
,所以原式继续化简为:
当
的时候,
就等价于求
在
处的导数。而函数
等同于函数
与函数
的复合函数,因此
而
,
,因此
所以
即
定义:假设函数 是二阶可微的(对于所有
,
矩阵都存在定义),当且仅当
为凸集且对于所有
,都有
时,可以称函数
是凸函数。
需要注意的是,此处的符号 与上文多面体定义中用到的符号含义不同,此处的
表示半正定,而非逐元素不等。
实际上,凸性的一阶条件和二阶条件是等价的,由凸性的一阶条件可以推出凸性的二阶条件。先写出函数 在
处的二阶泰勒展开:
令
, 则有
此处式中的余项
在
时相对于
是更高阶的无穷小,所以当凸性的一阶条件
成立时,此处的二阶项
。其中,
为函数
在点
处的
矩阵,
表示
矩阵为半正定。由
矩阵的定义
可知,此时凸性的二阶条件
成立。
为了便于理解,可以将输入变量 设为一维的。此时凸性的二阶条件就等同于函数
的二阶导数
。
更多关于凸函数的二阶条件以及 矩阵的讨论可以参考这个问题:怎么理解二阶偏导与凸函数的Hessian矩阵是半正定的?
给定凸函数 以及一个实数
,集合
定义为:
换句话说,对于函数
来说,
是所有符合条件
的点的集合。
是个凸集,这一点可以利用定义进行证明。
- 指数函数
- 负对数函数
- 仿射函数:由于仿射函数项的最高次数为1,因此可知仿射函数的
矩阵
(可以将
矩阵类比于函数的二阶导数),而由于零矩阵即是半正定的又是半负定的,所以仿射函数既是凸函数又是凹函数。实际上,仿射函数是唯一一种既凹又凸的函数
- 二次函数:设函数
为
,其中
,
,
。根据上文提及的二次函数的
矩阵知
,因此由凸性的二阶条件可知,函数
的凸性取决于矩阵
是否为半正定的
- 范数:设函数
是
上的范数,根据三角不等式以及范数的齐次性,对于任何
,
,有
注意,此处函数的凸性无法利用凸性的一阶条件以及二阶条件进行证明,因为范数本身可能并不是处处可微的
- 凸函数的非负加权和:设函数
为凸函数,
为非负实数,设函数
为
则函数
是凸函数,因为
在对凸函数以及凸集有了充分的认知以后,是时候来对凸优化问题进行定义了。凸优化问题有着如下形式: 即函数的输入
服从约束集合
,而问题的目标为最小化
。此处函数
为凸函数,集合
为凸集,
为优化变量。这种写法稍显不够清晰,因此将上述形式进行重写:
此处函数
为凸函数,函数
为凸函数,函数
为仿射函数,
为优化变量。值得注意的是此处的不等式中不等号的方向。函数
必须小于等于零,这是因为凸函数
的
是一个凸集,这样才能保证当所有不等式约束同时成立时,约束下的可行区域依然是凸集(凸集的交集依然是凸集)。此外,此处的等式一定且只能是仿射函数,直觉上来说,等式
等价于两个不等式
与
,进一步推导知其等价于不等式
与
。此时,拆解后的等式约束就可以全部归纳到前面的不等式约束
中,按照不等式约束的条件,所有函数
都是凸函数,所以函数
都是凸函数,即函数
既凸又凹,而唯一一类又凸又凹的函数就是仿射函数,所以
一定且只能是仿射函数。
有了凸优化问题的定义之后,就能对局部最优点以及全局最优点进行定义了。
局部最优点的定义:如果一个点 服从优化问题的约束,且对于所有服从优化问题约束的点
,都存在某个
使所有服从约束
的点
满足
,那么点
可以被称为局部最优点。
全局最优点的定义:如果一个点 服从优化问题的约束,且对于所有服从优化问题约束的点
都存在
,那么
可以被称为全局最优点。
凸优化问题的关键在于,凸优化问题中的所有局部最优点都是全局最优的。可以利用反证法对其这一点进行证明。假设点 是凸优化问题中的一个局部最优点而非全局最优点,那么一定存在另一个服从优化问题约束的点
使
。根据局部最优点的定义,不存在能使约束
与
同时成立且服从优化问题约束的点
。但假设通过选择
并选择
,那么有:
并且
即
,而这与局部最优的定义相悖。所以点
一定是全局最优点。



