凸分析和凸优化有什么推荐的教材吗？_盛煌-盛煌娱乐-盛煌商务站

盛煌登录

/public/upload/system/2018/07/26/f743a52e720d8579f61650d7ca7a63a0.jpg

邮箱：: 广东省广州市天河区88号

电话：: /public/upload/system/2018/07/26/f743a52e720d8579f61650d7ca7a63a0.jpg

传真：: /public/upload/system/2018/07/26/fe272790a21a4d3e1e670f37534a3a7d.png

手机：: 13800000000

地址：: 1234567890

盛煌APP下载

当前位置：首页 > 盛煌APP下载

凸分析和凸优化有什么推荐的教材吗？　上传时间：2024-05-26 09:42:08

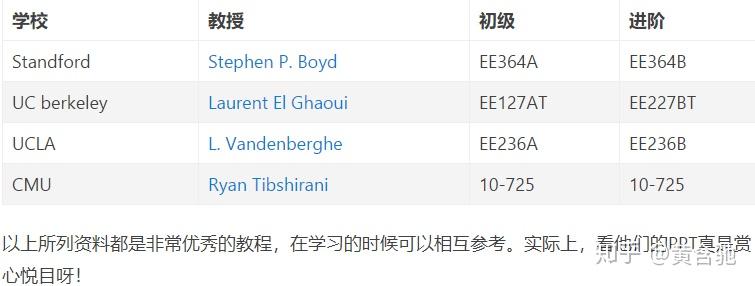
《凸分析》和《凸优化》啊。

R. T. Rockafellar. Convex Analysis. Princeton, 1970.

S. Boyd and L. Vandenberghe. Convex Optimization. Cambridge, 2004.

少年，如今这个时代，单纯看书是不够的，请配合大牛的课程vedio一起学习！

（1）如楼上所说的，S. Boyd and L. Vandenberghe. 写的书 <Convex Optimization> 听说不错，我没看过... 然后S.Boyd 还给了配套的课程video可以一起学习 EE364a: Lecture Videos, 听说有新版本的video ，我没找到。

( 2 ) CMU 有个老师叫Ryan T 开了门Convex Optimization上过一些，感觉不错，我没看完，你可以试试，这里是链接：Convex Optimization 。

（3）Nesterov 的《Introductory Lectures on Convex Programming》推荐你看看前两章引入convex 概念的，写的挺好的。我写过一篇读这个文章的小笔记，你可以辅助着看：从Nesterov的角度看：我们为什么要研究凸优化？ - 知乎专栏

（4）关于 Stochastic 的算法我还推荐你看看 L Bottou 的 [1606.04838]Optimization Methods for Large-Scale Machine Learning 确实写的不错，我看了开头，写了点读书心得，可以对照着看看为什么我们更宠爱“随机”梯度下降？

（5）评论里 @各人给出的意见感觉还蛮中肯的，故复录于下：入门凸优化的话看el ghaoui那本optimization models可能好点，毕竟从线代开始讲，而且很多proof和一些涉及到几何/分析的东西都被带过了。凸分析必须boyd了，虽然那本实际上还是require不少mathematical maturity的。boyd那本书我非常喜欢，一点废话都没有解释的特别清楚，书后习题也非常有意思，我自己是把lp/qp/duality那几章全部刷了一遍。

如果纯粹学习，看看（1）就够了，想做做research 那么（2）（3）（4）都看完了，也不够，哈哈哈哈哈！！！

最后，你如果热情不减，还想继续了解优化算法，欢迎关注我 @未名和我的专栏。。。我会写写自己学习凸\\非凸优化的心得，大家一起学习交流。

非凸优化学习之路 - 知乎专栏

第一篇文章是：从Nesterov的角度看：我们为什么要研究凸优化？ - 知乎专栏

第二篇文章是：非凸优化基石：Lipschitz Condition - 知乎专栏

第三篇文章是：当我们谈论收敛速度时，我们都在谈什么？ - 知乎专栏

最最后，从大量知识的喜悦中脱离一下，点个赞呗。

泻药@王哲

一句话概括的话，凸分析主要研究凸集和凸函数的各种拓扑和分析性质，凸优化研究凸问题的最优性条件，设计求解算法并分析其迭代复杂度和计算复杂度。

好专著通常出自这两个领域的大师。记住这些凸分析和凸优化大师的名号：R. T. Rockafellar，Hiriart-Urruty，A Nemirovski ，Y. Nesterov， Yinyu Ye(叶荫宇)...更多的看 John von Neumann Theory Prize 历年获奖的大师名单。当然，也不能排除一些非top-class的数学家写作技巧很好，写的入门级教材图文结合，形象易懂(嗯，我这里指的主要是Y. Nesterov的论文很难读).....

入门级

S. Boyd and L. Vandenberghe. Convex Optimization[M]. Cambridge, 2004.

Güler O. Foundations of Optimization[M]. Springer New York, 2010.

Bahlak S, Gazalet J, Lefebvre J E, et al. Convex Optimization: Algorithms and Complexity[J]. Foundations & Trends? in Machine Learning, 2014, 8(3-4):231-357.

进阶版

A Nemirovski 个人主页上一系列的凸优化的slides

Ben-Tal A, Nemirovski A. Lectures on modern convex optimization[M]. SIAM, 2001.

Hiriart-Urruty J B, Lemaréchal C. Fundamentals of Convex Analysis[M]. Grundlehren Text Editions, 2004, 24(2):288-294.

R. T. Rockafellar. Convex Analysis[M]. Princeton, 1970.

Hiriart-Urruty J B, Lemaréchal C. Convex analysis and minimization algorithms[M]. Springer-Verlag, 1993.

Nesterov Y. Introductory Lectures on Convex Optimization[M]. Springer, 2014.

内点算法

Nesterov I E, Nemirovski? A S. Interior Point Polynomial Algorithms in Convex Programming[M]. SIAM, 1994.

Ye Y. Interior point algorithms: theory and analysis[M]. John Wiley & Sons, Inc. 1997.

Wright S J. Primal-dual interior-point methods[M]. SIAM, 1997.

Roos C, Terlaky T, Vial J P. Interior Point Methods for Linear Optimization[M]. Springer, 2006.

如果不读博士做理论研究，好像基本上也不需要凸分析了；学术圈子里认真待个两三年，主动去了解这个领域，这些大师的名字会反复出现在论文和参考文献里，读读他们的专著就很有必要了...当然还有很多大牛，他们只写论文，没空写专著的，这时候就应该好好读论文了...

①备受瞩目的Stephen Boyd的Convex Optimization

官方网站：

Convex Optimization - Boyd and Vandenberghe

配套matlab代码：

additional_exercises

我个人认为，这本书作为凸优化的入门图书其实并不适合，主要原因有两点：
内容太多，中文版《凸优化》将近700页，对于初学者，学习主干内容就可以了，可能也就200多页，但是前提是需要有人教学。
算法内容有限，很多同学学习凸优化的目的可能更想学习算法部分，但该书主要讲解内点法，对于现在热门的次梯度法，近邻算子法等没有涉猎。
有更合适的入门书籍《Optimization Model》.

作者：jack0077555
链接：https://www.jianshu.com/p/282116480e80

②本学期凸优化slides及李东风老师的统计计算（最后一张，八十多面，超级精简且说人话）

满200的话拉您进2群，加我微信 jjnuxjp5x

链接: https://pan.baidu.com/s/1GVj1Q1fAsW_XyEfLPzODxA 提取码: c5pv

若非要深入研究，资料真的很棒的

eg:

③见北大凸优化课程主页http://bicmr.pku.edu.cn/~wenzw/opt-2018-fall.html

④

本课程整理自中国科学技术大学2011年课程《最优化理论》，

主讲人：凌青老师

https://cse.sysu.edu.cn/content/3112

课程主要教材

Boyd S , Vandenberghe L . Convex Optimization. Cambridge University Press, 2004.

https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf

课程视频网上有很多，这里只放一个链接

https://www.bilibili.com/video/BV1Jt411p7jE

本文彩色插图由 @陌上疏影凉提供
本教程已收录到专栏

中科大凸优化知识点笔记

本文内容对应视频lec25-28，本文对应4个知识点，分别为

线性规划
二次规划
半定规划
多目标优化

linear program：目标与约束均为线性

? $\\min \\quad c^Tx+d ,\\quad c\\in \\mathbb{R}^n,d\\in \\mathbb{R}$

? $s.t. \\quad Gx\\leq h,G\\in \\mathbb{R}^{m\ imes n}, h\\in \\mathbb{R}^m$

? $Ax=b,A\\in \\mathbb{R}^{k\ imes n},b\\in \\mathbb{R}^k$

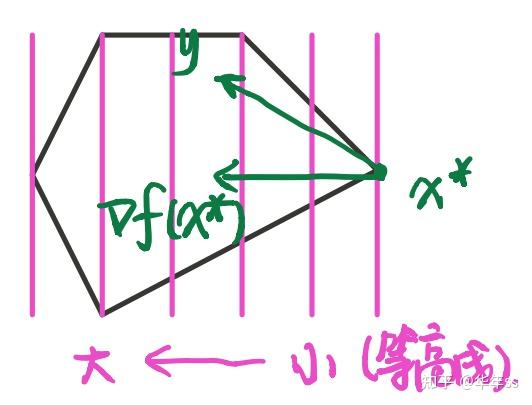
根据一阶最优条件线性规划的解在边界上

线性规划的等价变换
$\\min \\quad c^Tx+d$
$s.t. \\quad Gx+s=h$
? $Ax=b$
? $s\\geq 0$
上式中 $x$ 可写为 $x=x^+-x^-$ ，这里 $x^+,x^-$ 都大于等于0
等价形式为
$\\min \\quad c^Tx^+-c^Tx^-+d$
$s.t.\\quad Gx^+-Gx^-+s=h$
? $Ax^+-Ax^-=b$
? $s\\geq0,x^+\\geq 0,x^-\\geq0$
线性规划问题可由matlab中linprog函数求解

典型的线性规划问题有物流调度、食谱问题等。这里以食谱问题为例，
例1，现要以最低的总价购买一批食物，要求总计食物中的 $m$ 种营养元素分别不小于 $b_1,\\dots, b_m$ ，有 $n$ 种食物，第 $j$ 种食物中第 $m$ 种营养为 $a_{1j},\\dots,a_{mj },\\forall j=1,\\dots,n$ ，每种食物价格为 $c_j$

写为优化问题的形式，设每种食物量分别为 $x_1,\\dots,x_n$
$\\min \\quad \\sum_jc_jx_j$
$s.t.\\quad \\sum_ja_{ij}x_j\\geq b_j,\\forall i$

? $x_j\\geq 0,\\forall j$

? 例2，线性分数规划(linear fractional programming)

? $\\min \\quad f_0(x)=\\frac{c^Tx+d}{e^Tx+f}$ ， $dom\\quad f_0=\\{x|e^Tx+f>0\\}$

? $s.t. \\quad Gx\\leq h$

? $Ax=b$

? 这个问题不是标准的凸问题，可通过如下转化变为线性规划问题，令 $y=\\frac{x}{e^Tx+f},z=\\frac{1}{e^Tx+f}$

? $\\min \\quad c^Ty+dz$

? $s.t. \\quad Gy-hz\\leq0,e^x+fz=1,Ay-bz=0,z\\geq0$

(quadratic programming, QP)目标函数为二次函数，约束为放射约束
$\\min \\quad \\frac{1}{2}x^TPx+q^Tx+r$ 凸 $P\\in S^n_+$

? $s.t.\\quad Qx\\leq h,Ax=b$

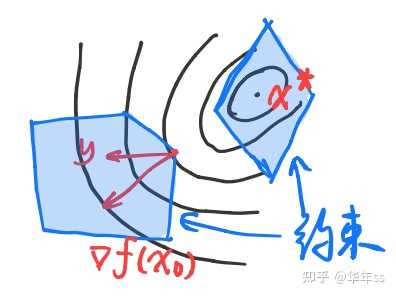
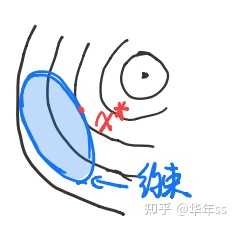
QP问题最优解不一定在约束的边上，如下图

二次约束二次规划(Quadratic constraint quadratic programming, QCQP)
$\\min \\quad \\frac{1}{2}x^TPx+q^Tx+r,P\\in S^n_+$
$s.t.\\quad \\frac{1}{2}x^TP_ix+q_i^Tx+r_i\\leq 0,P_i\\in S^n_+,\\forall i$
? $Ax=b$

例1，带噪声的测量系统 $b=Ax+e$
$\\hat x=\\arg\\min\\limits_x \\|b-Ax\\|_2$

$=\\arg\\min\\limits_x \\|b-Ax\\|_2^2$

? $=\\arg\\min\\limits_x x^TA^TAx-2b^TAx+b^Tb$

? 这是典型的无约束QP问题，解为 $x^*=(A^TA)^{-1}A^Tb$

例2，若 $x$ 稀疏( $L_1$ -Regularized least squares)
$\\hat x=\\arg\\min\\limits_x \\|b-Ax\\|_2^2+\\lambda_0 \\|x\\|_0$
? $=\\arg\\min\\limits_x \\|b-Ax\\|_2^2+\\lambda_0 \\|x\\|_1$
例3，( $L_2$ -Regularized least squares)岭回归

? $\\hat x=\\arg\\min\\limits_x \\|b-Ax\\|_2^2+\\lambda_0 \\|x\\|_2^2$

? 以上等价于 $\\arg\\min\\limits_x \\|b-Ax\\|_2^2$ ， $s.t.\\quad \\|x\\|^2\\leq \ heta,\ heta\\geq 0$ ，这是一个QCQP问题

Semi-definite Programming, SDP 可写为
$\\min \\quad tr(CX)$
$s.t. \\quad tr(A_iX)=b_i,i=1,\\dots,p$
? $x\\succeq0$
其中 $C,A\\in \\mathbb{S}^n$
特例：对角矩阵 $diag \\{x\\}$
$\\min \\quad (diag \\{x\\})^Tdiag \\{x\\}$
$s.t. \\quad (diga\\{A_i\\})^Tdiag \\{x\\}=b_i,i=1,\\dots,p$
? $diag\\{x\\}\\geq 0$
仅有不等式约束的半定规划问题
$\\min \\quad c^Tx$
$s.t. \\quad x_1A_1+\\dots,+x_n A_n\\preceq B$
其中 $B,A\\in \\mathbb{S}^k$
例，求最小化矩阵 $A(x)=A+x_1A_1+\\dots+x_nA_n,A_i\\in \\mathbb{R}^{p\ imes q}$ 最大奇异值对应的 $x$

$\\min \\|A(x)\\|_2$

$\\|A(x)\\|_2 \\leq \\sqrt s,s>0$ 等价于 $A^T(x)A(x)-sI\\preceq 0$

以上问题可转化为

$\\min \\sqrt s$

$s.t. A^T(x)A(x)-sI\\preceq 0$

令 $t^2=s$ ，则以上问题可转化为

$\\min t$

$s.t. | tI \\quad A(x)|$

? $\\succeq 0$

? $| A^T(x) \\quad tI|$

? $t\\geq 0$

$\\min \\quad f_0 (x)$ 其中 $f_0:\\mathbb{R}^n\\rightarrow \\mathbb{R}^q$
$s.t. \\quad f_i(x)\\leq 0$
? $h_i(x)=0$
例如，投资要在总成本限制下，最小化风险，最大化收益；发展要在一定资源限制下，最大化发展速度与发展质量。
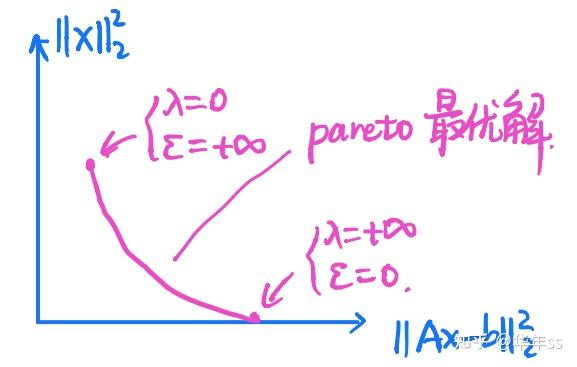
此时有多个目标，通常在某个指标上变好，就会在另外一个指标上变差，权衡不同目标，得出最优解的集合称为帕累托曲面(Pareto front)