基于鲸鱼优化算法的Simulink仿真模型参数优化

前言：我们在用simulink进行仿真模型的时候，通常会遇到一些参数需要手动调节，如PID参数、模糊PID参数等，非常耗时，且难以得到最优的参数，得到最优的仿真效果。本文将以鲸鱼优化算法（WOA）优化PID仿真模型为例，阐述如何利用智能优化算法联合simulink仿真模型进行仿真模型的参数优化，其他的算法和模型可以以此类推。

鲸鱼优化算法(WOA)是一种元启发式优化算法，是 2016 年由澳大利亚格里菲斯大学的Mirjalili 等提出的一种新的群体智能优化算法，其优点在于操作简单，调整的参数少一种新的模拟座头鲸狩猎行为的元启发式优化算法(鲸鱼优化算法，WOA)。其他群优化算法相比的主要区别在于，采用随机或最佳搜索代理来模拟捕猎行为，并使用螺旋来模拟座头鲸的泡泡网攻击机制。

原论文+代码下载：

https://pan.baidu.com/s/1GpxqSjgoSh3Fplz3dp9OSg?pwd=i21f?
提取码：i21f

在 WOA 算法中，每只座头鲸的位置代表一个可行解。在海洋活动中，座头鲸有着一种特殊的狩猎方法，这种觅食行为称为bubble-net 捕食策略?，其狩猎行为如下图所示：

1.1.1?包围猎物

座头鲸在狩猎时要包围猎物，作者根据行为特点提出了下面的数学模型：

$D=\left | CX^*(t)-X(t))) \right | \\ X(t+1)=X ^*(t)-AD$

式中： $t$ 是当前迭代次数； $A$ 和 $C$ 为表示系数 $X^*(t)$ 表示目前为止最好的鲸鱼位置向量， $X ( t )$ ?
表示当前鲸鱼的位置向量， $A$ 和 $C$ 由下式可得到

$A=2ar_1-a \\ C=2r_2 \\ a=2-\frac{at}{T_{max}}$

其中， $r_1$ 和 $r_2$ ?是(0,1)中的随机数，a 的值从 2到 0 线性下降， $t$ 表示当前的迭代次数， $T_{max}$ 为最大迭代次数。
?

1.1.2 狩猎行为

?在搜索猎物时，其数学模型如下：根据座头鲸的狩猎行为，它是以螺旋运动游向猎物，故狩猎行为的数学模型如下：

$X(t+1)=X^t(t)+D_pe^{bl}\cos (2\pi \l)$

$X(t+1)=\begin{Bmatrix}X^*(t)-AD,p<P_i \\ X(t)=X^*(t)+D_pe^bl \cos(2\pi \l) \end{Bmatrix}$

攻击猎物时，在数学模型上靠近猎物设定了减小a的值，这样A的波动范围也随a下降。在迭代过程中当a的值从2到0下降时，A 是在[?a,a]内的随机值，当A 的值在[?1,1]内时，鲸鱼的下一个位置可以是它现在的位置和猎物的位置之间的任意位置，算法设定当A<1 时，鲸鱼向猎物发起攻击。
?

1.1.3 搜索猎物

在搜索猎物时，其数学模型如下：

$D=\left | CX_{rand}-Xt \right | \\ X(t+1)=X_{rand}-AD$

?其中 $X_{rand}$ 是随机选择的鲸鱼位置向量，算法设定当1A≥1 时，随机选择一个搜索代理，根据随机选择的鲸鱼位置来更新其他鲸鱼的位置，迫使鲸鱼偏离猎物，借此找到一个更合适的猎物，这样可以加强算法的勘探能力使 WOA 算法能够进行全局搜索。
?

（1）初始化参数：即鲸鱼种群规模大小 $SN$ ，最大迭代次数 $T_{max}$ ；
（2）算法初始化鲸鱼种群的位置；
（3）计算每一头鲸鱼相应的适应度值，根据适应度值的大小排序，并选取 $SN$ 个作为初始种群；
（4）计算出 $SN$ 个个体适应度值的大小，找出适应度值最小的个体位置作为最优位置；
（5）更新下一代的位置；
（6）若达到终止条件，则输出最优个体，即算法找到的最优解；否则，返回步骤（4）。
?

本文以下图所示的PID仿真模型为例，讲解如何利用WOA优化算法对仿真模型中的参数进行优化，首先需要在Simulink中搭建下图所示的仿真模型，命令为pid_mode.mdl.

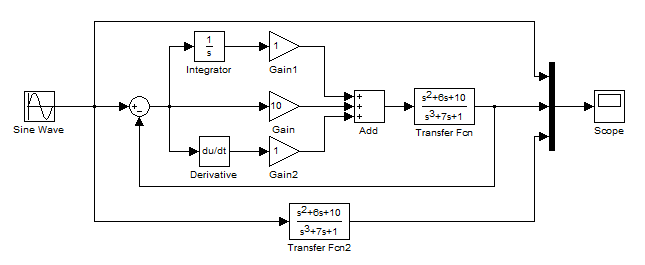
?通过以下代码，我们可以通过以下代码完成对模型中的参数值进行值的设定和获得仿真结果。

通过上述方法获得仿真结果后，我们需要对结果进行性能评价，常见的评价函数有以下几种：

ITAE：时间乘以误差绝对值积分(ITAE)的性能指标是一种具有很好工程实用性和选择性的控制系统性能评价指标.ITAE指标是综合描述系统动态性能比较有效的指标。

$J(ITAE)=\int_{ - \infty }^{ + \infty } {t \left |e(t) \right |dt}$

ITSE：

$J(ITSE)=\int_{ - \infty }^{ + \infty } {t e^2(t) dt}$

ISP

$J(ISP)=\int_{ - \infty }^{ + \infty } {\left [ (1-\alpha) e^2(t) +\alpha(\Delta u^2(t)))) \right ] dt}$

通过上述评价函数，我们可以将仿真模型与智能优化算法联合起来，进行优化。整个流程大致为：

优化算法生成初始种群，种群中的每个值表示PID参数的一种解->目标函数将种群中的每组参数通过调用仿真模型得到仿真结果，再计算出评价指标作为优化算法的适应度值，优化算法根据适应度值对种群进行更新，然后进行下一次迭代，知道得到最优的PID参数。

通过上述方法，我们利用WOA算法迭代优化了100代，可以看到结果如下：

本文只是以WOA优化算法优化PID仿真模型为例，其他的算法优化其他的仿真模型原理类似，只需要设定好模型待寻优的参数，通过选取合适的评价指标，再与优化算法联动，就可以完成优化。如果你对其他问题有所困惑，欢迎私信与我联系。

[1]Seyedali Mirjalili,Andrew Lewis. The Whale Optimization Algorithm[J]. Advances in Engineering Software,2016,95.

上一篇：12号金蝉传说升级，白虎志返场，免费皮肤3选1，瑶妹冬日限定绝美

下一篇：【三重四创五优化】“三重四创五优化”到底指什么？

返回列表