最近在看Leon Bottou的大规模机器学习中的优化算法，发现里面有一些算法不太好理解，所以自己找了一些文章看了看，决定把SAG,SVRG,SAGA三种算法介绍一下。

对于这三种方法，我们主要目的是希望达到线性收敛的结果。

我们都知道，在机器学习中，最常用的优化算法就是SGD(随机梯度下降算法)，我们发现它在但是SGD由于每次迭代方向都是随机选择的，所以产生了下降方向的噪音的方差。正是由于这个方差的存在，所以导致了SGD在每次迭代（使用固定步长 ）时，最终是收敛不到最优值的，最优间隔最终趋于一个和方差有关的定值。为了克服这一点，我们采取一种办法，是想要让方差呈递减趋势下降，那么最终算法的将会以线性速度收敛于最优值。下面这个定理时论文中的结果：

根据这个想法，我们主要有SAG,SVRG,SAGA三种最常用的算法。

我们首先来介绍SVRG(stochastic variance reduced gradient),该方法是在一个循环中进行的，在每次循环之前， 可用于计算

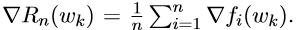
然后我们初始化 ,然后进行一系列由j引导的m次内循环，它的更新格式是：

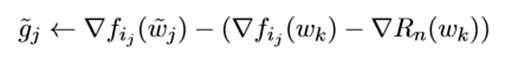
是随机选取的，而且我们可以发现 是 的一个无偏估计，这样我们就可以和全梯度下降（GD）联系起来。方差会减小(在后面会说为什么)，所以最终该算法会以线性收敛到最优值。他的具体算法如下：

从算法过程来看，我们也很明显可以看到SVRG的计算量相比较SGD大得多，所以文中作者使用了相同的计算量的办法来比较SAG和SVRG算法的区别(就是说，在SGD和SVRG同时都计算了相同次，来看它们各自算法的优越），我们有如下图：

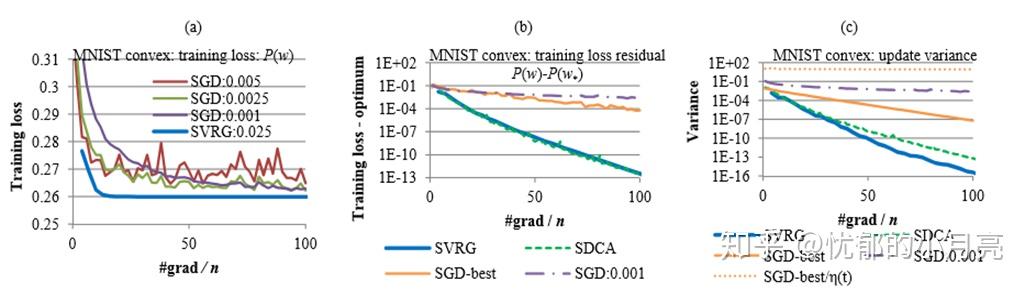
主要观看图a和图c，很明显SVRG相对于SGD来说在最优值附近几乎没有震荡，既没有噪音，但是SGD在最优值附近震荡明显。而且在图c中，可以看到SVRG下降方向的方差最终趋于零，明显比SGD小。

提出SAG（Stochastic Average Gradient）主要是它既有SGD算法计算量小的特点，又具有像FGD一样的线性收敛速度。它的一般形式如下：

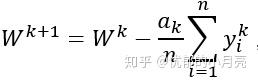
这里的 是方向，其中中每次迭代中任意选取 ，我们有：

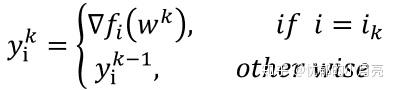
这样，我们可以看到，每次迭代时，通过访问 并为每个索引i保留最近计算出的梯度值的储存，具体算法如下：(我们令 )

（加一下自己的理解，SAG就是一开始我们先在 处计算每个梯度( ), 一共有n个，然后把这n个梯度全部存储到计算机中。在每次迭代时，我们随机选i，然后对于内存里面第i个样本的损失函数 ,我们计算出 ，使用它替换掉原来位置 的梯度 ，然后我们就很好的解释了公式 .它有点像SGD，但是每次计算中我们需要涉及到两个梯度，而且都将新计算出来的梯度取代原来相同位置的梯度，并且保存该梯度。）

对于SAG，我们并没有实际理论说明它降低了方差，但是我们有理论证明它在步长 时线性收敛于最优值。

SAGA算法是SAG算法的一个加速版本，和SAG一样，它既不在一个循环里面操作，也不计算批量梯度(除了在初始点)，在每次迭代中，它都计算随机向量 作为前期迭代中随机梯度的平均值。

特别的，在迭代k次中，算法将会存储 ,对于前期所有的 ,其中 表示 计算出的最近的一次迭代 。整数 是任意选取的。并且随机方向为：

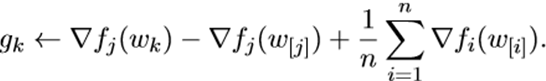
看 的结构,也可以发现他也是 的一个无偏估计。而且每次都需要存储n个梯度。他的具体算法如下：

SAGA也减少了噪音的影响。(SAGA和SAG的区别就是一个是无偏估计，一个不是)